상관계수(Correlation coefficient)
-두 변수가 얼마나 강하게 연결되어 있는지를 숫자로 표현
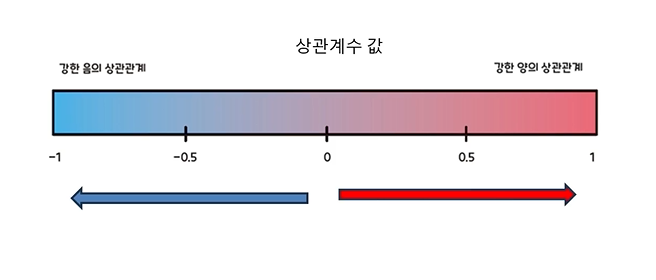
- 1에 가까울수록 두 변수가 같이 움직임
- -1에 가까울수록 반대로 움직임
- -0이면 서 관련 없음
- 피어슨 상관분석(pearson correlation analysis): 가장 일반적인 상관 분석 방법
- 스피어만 상관분석(Spearman correlation analysis): 두 변수가 정규성을 보이지 않을떄 사용하기 적합
- 켄달 상관분석(Kendall correlation analysis): 스피어만 상관분석과 비슷하나 표본 데이터가 적고 동점이 많을때 사용하기 적합
<차이점>

1. 상관분석 데이터 준비
import pandas as pd
import matplotlib.pyplot as plt
# 리스트에 데이터 삽입하기
X = [1, 2, 3, 4, 5]
Y_linear = [2, 4, 6, 8, 10] # 선형 데이터
# 리스트를 데이터프레임으로 변환하기
data = {'X': X, 'Y_선형': Y_linear}
df = pd.DataFrame(data)
df
2. 그래프
# 그래프그리기
df.plot(x='X', y='Y_선형' )
plt.show()
3. 피어슨 상관분석
# 피어슨상관분석수행하기(X와Y선형)
coef_p = df.corr(method='pearson')
print("피어슨상관계수(X와Y_linear):")
print(coef_p)
4. 스피어만 상관분석
# 스피어만상관분석수행하기(X와Y선형)
coef_s = df.corr(method='spearman')
print("\n스피어만상관계수(X와Y_linear):")
print(coef_s)
5. 켄달 상관분석
# 켄달상관분석수행하기(X와Y선형)
coef_k = df.corr(method='kendall')
print("\n켄달 상관계수(X와Y_linear):")
print(coef_k)
#고수정 교수님 수업자료 참고
'데이터 분석' 카테고리의 다른 글
| 데이터 전처리 (0) | 2024.11.26 |
|---|---|
| 웹 크롤링 기초 (0) | 2024.11.23 |
| 1. 데이터 분석 (0) | 2024.09.21 |
| python기초 정리 (0) | 2024.09.21 |
